Mellanstadiematematiken som hjälper dig att parkera
Har du bil? I så fall har du nog mer än en gång riktat en tacksam tanke till bilens parkeringshjälp – du vet det där taktfasta pipandet som kan guida dig in i en omöjlig parkeringsficka. Det du kanske inte kände till är att du då också tackar en lika välkänd som undangömd matematisk formel. En formel som kan konststycket att förvandla avstånd till tid.
Fickparkeringsmatematik
Fram och bak på våra moderna bilar sitter så kallade ultraljudssensorer. De skickar ut ljudvågor i alla tänkbara riktningar, på frekvenser som inget mänskligt öra kan uppfatta.
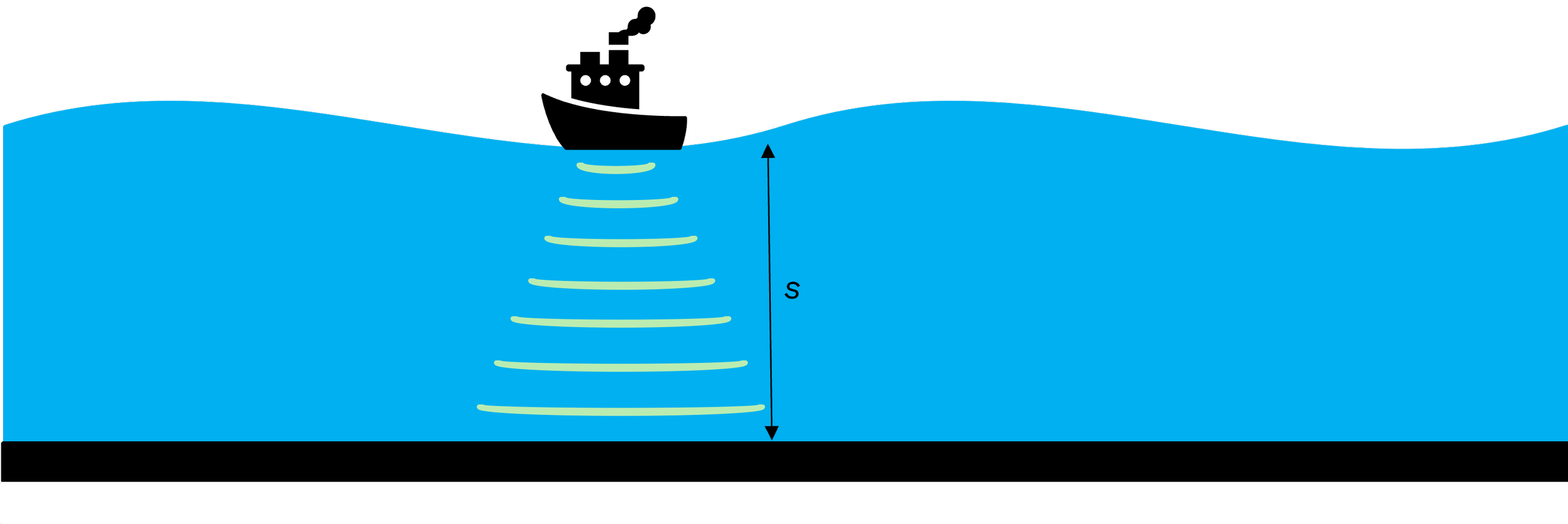
s är avståndet från bilen till omgivande föremål
Ljudvågorna studsar på de föremål som finns runt bilen och färdas sedan tillbaka till sensorn. Genom att mäta hur lång tid det tar för ljudvågorna att komma tillbaka, kan sensorn beräkna avståndet till de omgivande föremålen och rytmiskt börja pipa när du kommer för nära. Tricket? Lite klassrumsdoftande mellanstadiematematik.
Låt mig visa dig detaljerna.
Minns du formeln s = v ∙ t? Den säger att om något färdas med jämn hastighet så kan den tillryggalagda sträckan beräknas genom att multiplicera hastigheten med tiden.
s = v ∙ t s är sträckan, v är hastigheten och t är tiden
Ljudvågorna som bilens sensorer skickar ut färdas just i jämn hastighet, närmare bestämt 340 meter per sekund. Om vi multiplicerar 340 m/s med tiden i sekunder, får vi alltså reda på hur lång sträcka som ljudvågorna totalt har färdats sen de skickades ut.
s = 340 ∙ t
Men ljudvågorna har ju färdats både från bilen till föremålet och tillbaka, dvs. dubbelt så lång sträcka som vi är intresserade av. Därför måste vi dividera resultatet med 2 (*).
Om ljudvågorna studsar tillbaka till sensorn på två tusendels sekunder, ja, då är det en enkel match att räkna ut att föremålet du vill undvika är 0,34 meter bort.
s = 340 m/s · 0,002 s 2 = 0,34 m
Och parkeringshjälpen har börjat pipa för länge sen.
Havsdjup med ljudvågor
Men din bil är faktiskt inte den enda maskin som drar nytta av sambandet mellan sträcka, hastighet och tid. Samma idé används även för att mäta havsdjup. Genom att skicka ut ljudvågor och mäta hur lång tid det tar för ljudvågorna att komma tillbaka, kan ett ekolod ta reda på avståndet till botten.
Det enda ekolodstillverkaren behöver tänka på är att ljud färdas snabbare i vatten – ungefär med hastigheten 1 500 meter per sekund – så formeln kommer att se ut så här:
s = 1 500 · t 2
Medicinska ultraljudet
Mer förvånande är kanske att det är samma idé – samma formel – som ligger bakom det medicinska ultraljudet.
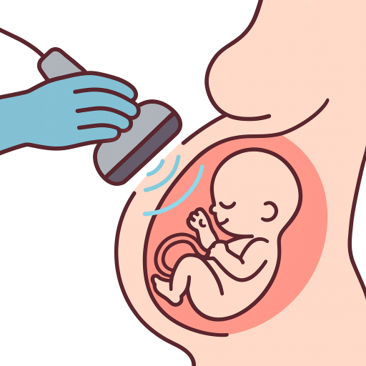
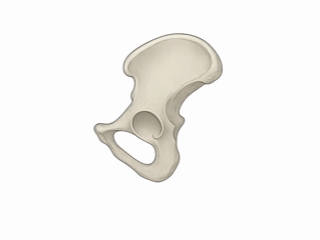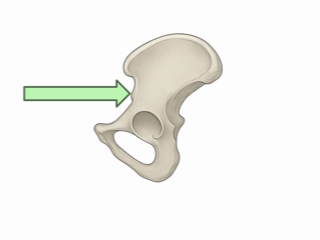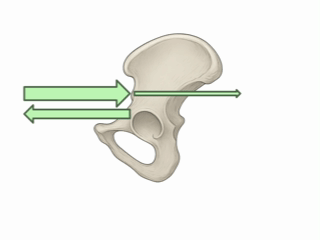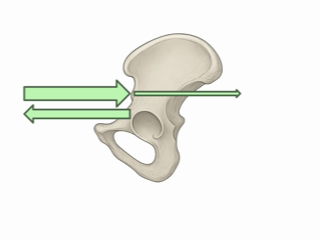
Säg att man vill göra en ultraljudsundersökning av ett foster. Med hjälp av en givare skickar man då in ultraljudsvågor i mammans mage. De här ljudvågorna kommer att röra sig in i kroppen. Men när de möter en ny vävnad, en ny struktur, så kommer en del av dem att reflekteras och studsa tillbaka till givaren.
Hur mycket av ljudvågorna som studsar tillbaka ger information om vilken typ av yta det är. Ben, till exempel, reflekterar en stor andel av ljudvågorna, medan muskler eller organ reflekterar en mycket mindre andel.
Ben reflekterar en stor andel av ljudvågorna
Organ reflekterar en mindre andel av ljudvågorna
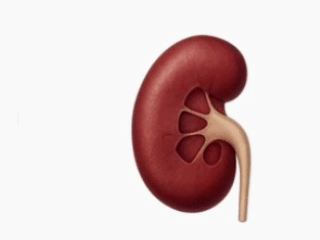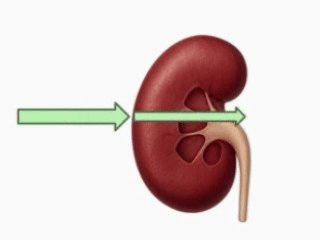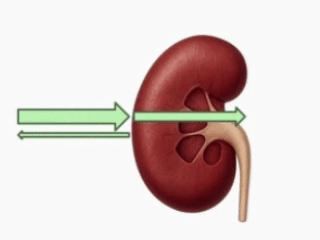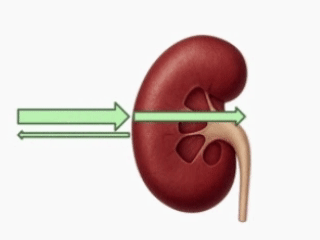
Den här informationen fångas upp av ultraljudsgivaren som mäter, både ekonas styrka och hur lång tid det tog för dem att komma tillbaka. Med hjälp av tiden kan givaren – med samma formel som tidigare – beräkna en sträcka, i det här fallet från vilket djup ekona reflekterades.
Givaren skulle till exempel kunna dra slutsatsen att den starkare ljudvågen reflekterades i en vävnad på bara 5 cm djup, medan den svagare ljudvågen tog längre tid på sig att komma tillbaka och därför reflekterades på ett längre avstånd, kanske 7 cm djup.
Med hjälp av tid kan givaren avgöra från vilket djup respektive ljudvåg reflekterades.
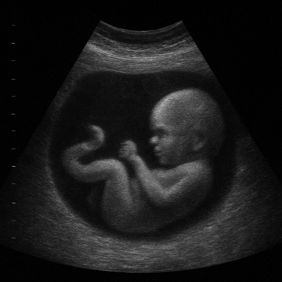
Den informationen används sedan för att skapa en ultraljudsbild, alltså en bild som visar vad som finns, på olika djup, framför ultraljudsgivaren. Grunda strukturer – alltså sådana som har kort avstånd till givaren – visas högst upp på skärmen, medan djupare strukturer visas längre ner.
En AI-renderad ultraljudsbild.
Det som avgör om det blir svart, grått eller vitt på ett visst avstånd från givaren är hur starkt ekot var från just den vävnaden. Starka ekon, t.ex. från en hård yta som ben, visas som vita strukturer på skärmen, medan blod, som i princip inte reflekterar några ljudvågor alls, markeras som svart. Och så är det en gråskala däremellan – en gråskala som kan visa alltifrån ett allvarligt sjukdomstillstånd till ett nytt bultande liv.
En nyckel – många dörrar
Hur är det möjligt att en enda formel kan hjälpa oss med så väsensskilda saker som att fickparkera, bestämma havsdjup och visa insidan av våra kroppar? Svaret är att matematik har förmågan att fånga ett fenomens grundläggande struktur. När den strukturen väl blivit synlig går den ofta att känna igen i andra situationer. Formeln som kan omvandla tid till avstånd gör till exempel gästspel även i byggarens lasermätare och i GPS:ens förmåga att lokalisera din position. För mig är just det en av matematikens superkrafter – att den med en och samma nyckel låter oss öppna helt olika dörrar.
(*) Ljudets hastighet i luft beror i sin tur på luftens temperatur enligt sambandet v = 331 + 0,61T, där v är hastigheten i m/s och T är temperaturen i grader Celsius. Sätter vi in det i sambandet s = v ∙ t får vi en formel som beror av både tid och temperatur:
s = (331 + 0,61T) · t 2